With its roots in the kinetic theory of gases, LBM evolved both from and independently of another closely related numerical method: the lattice gas method. LBM can also be viewed as a discrete representation of the Boltzmann equation from statistical physics.
Over the last couple of decades, there has been a tremendous amount of research and development in LBM (primarily within the academic community) and it has been successfully applied to several challenging problems.
The main selling point of LBM is the tremendously simple implementation. LBM is also extremely suitable for parallel computing because it is like an explicit time-marching scheme.
Comparisons with Navier-Stokes based CFD schemes is inevitable and both approaches have their strengths and weaknesses. The LBM is not a one-size-fits-all solution to all CFD problems.
 |
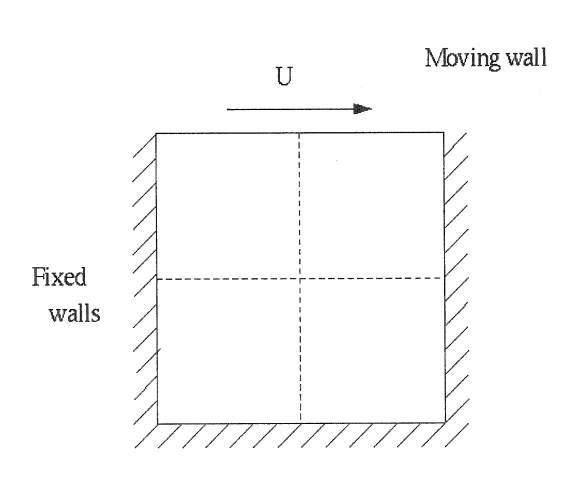2D driven cavity flowMy first ever LBM code, written when I was a student at Clemson University. This code solves the driven cavity flow problem for Re = 100 and prints out the horizontal and vertical centerline velocity profiles for validating the results. Source code (FORTRAN) |
 |
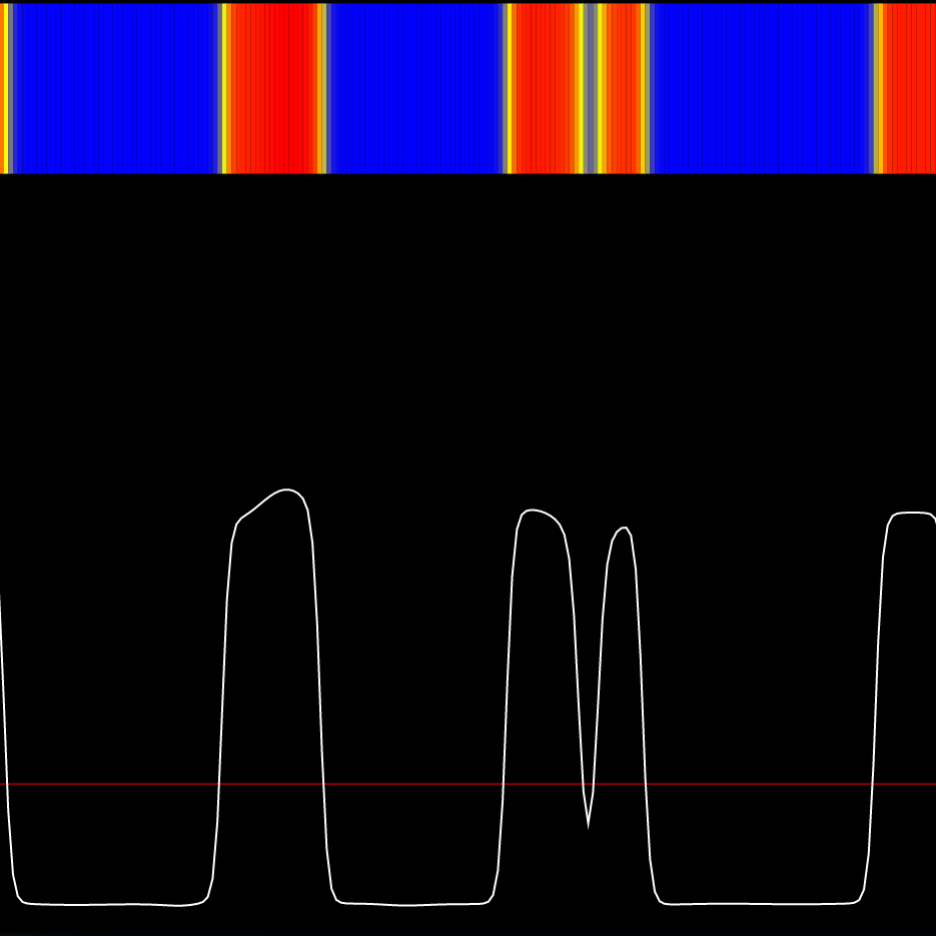1D multi-phase simulation (Shan & Chen, 1993)The solid white line is the fluid density. The simulation begins with a density value close to 0.693 (the horizontal red line), with some small perturbations. These perturbations grow over time because of attractive inter-particle forces, and the fluid separates into a high density (red) phase and a low density (blue) phase. Note that the total area under the white line does not change - mass is conserved. Source code (JavaScript) |
2D multi-phase simulation (Shan & Chen, 1993)The movie shows the density field evolving over time, starting from an average density of 0.693, with small perturbations. Like the 1D example, this simulation shows how the fluid separates into a liquid (red = high density) and a vapor (blue = low density) phase. To minimize system energy, smaller liquid drops coalesce together to form a single, large liquid drop. Source code (C++ with OpenGL) |
|
3D multi-phase simulation (Shan & Chen, 1993) - serial versionLike the 1D and 2D examples, the initially uniform fluid separates into a liquid and vapor phase. It is now best to use dedicated software for post-processing the results. I like to use XDMF+HDF5 for writing data and ParaView to see the output. The shape changes (morphology development) are driven by interfacial forces, which try to minimize the total surface area. The final, stable structure could be spherical drops, cylindrical fibers or an even more interesting beast - the Schwarz-P surface! Source code (C++, XDMF, HDF5) |
|
3D multi-phase simulation (Shan & Chen, 1993) - parallel version (MPI)This tutorial implements the algorithm in parallel using the message passing interface (MPI) library. Calculations in each sub-domain are handled by a different MPI rank, with appropriate inter-domain communication at the boundaries. The movie shows a cubical domain partitioned into 8 smaller cubes. The slight overlap between domains is because of "ghost layers", used for storing information from neighboring ranks. Source code (C++, MPI, XDMF, HDF5) |
Several interesting technologies for computer graphics and scientific computation exist in the modern workplace. Some, like OpenGL are relatively old and first appeared in the early to mid 1990s.
Objective-C was originally developed in the early 1980s, but is popular recently because it is the primary language for developing applications for the iPhone, iPad and Mac.
Both CUDA and OpenCL are relatively new and are concerned with speeding up any data-parallel calculations by using graphics processing units (GPUs) or other accelerators.
Although many of these technologies may seem completely unrelated, they can be combined with each other to create amazing applications. These tutorials will help you get started playing with all these tools.
 |
This is where you learn how to render 2D and 3D graphics and animation using OpenGL. This is the de-facto industry standard for rendering heavy-duty graphics. A subset of this API (called OpenGL-ES) is available for use with embedded systems - iPhones, iPad etc. - and we will look at some OpenGL-ES examples in the Objective-C tutorials. |
 |
Interested in developing games and apps for the iPhone and iPad? Start your journey by learning about Objective-C using this set of simple tutorials. Early on, the tutorials are completely command-line based and can be compiled and run using the terminal. Later on, we begin to use Apple's Xcode IDE to build iOS applications, including games. |
 |
Learn how to use NVIDIA's CUDA toolkit to accelerate your data-parallel applications and harness the true power of your desktop and/or laptop. In these tutorials, you will learn how to use CUDA to speed-up several applications, including a 2D Heat Transfer code, a 2D lattice Boltzmann simulation and an OpenGL graphics application to explore the Mandelbrot set. |
 |
OpenCL is the cross-platform alternative to CUDA, meaning it can run not only on NVIDIA GPUs, but almost any other GPUs, including the capacity to run parallel jobs on a combination of CPUs and GPUs. |